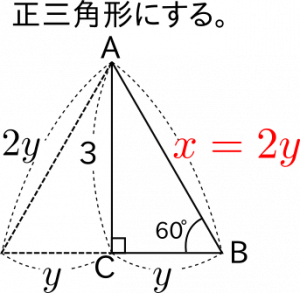さぁ、３学期が始まりました。つまり、中３にとっては、受験シーズン到来ということです。

受験勉強のコツです。

受験の数学で必須項目の一つに「三平方の定理」があります。

$a^2+b^2=c^2$

です。（ここで、直角に対する辺cが斜辺です。）

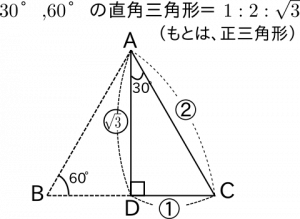
さらに、応用問題でよく利用される辺の比があります。そのひとつが、$1:2:\sqrt{3}$です。30゜、60゜の直角三角形の辺の比です。

これを使って次の辺$x,y$の長さを求めてみます。

【$x$を求める式】$AC:AB=\sqrt{3}:2より、\\\begin{align}3:x&=\sqrt{3}:2\nonumber\\\sqrt{3}x&=6\nonumber\\x&=\frac{6}{\sqrt{3}}=2\sqrt{3}\tag{答}\end{align}$

【$y$を求める式。】$AC:BC=\sqrt{3}:1より、\\\begin{align}3:y&=\sqrt{3}:1\nonumber\\\sqrt{3}y&=3\nonumber\\y&=\frac{3}{\sqrt{3}}=\sqrt{3}\tag{答}\end{align}$

どうですか？「まぁ、簡単ですね。」「まぁ、なんとか分かるね。」という人は大丈夫です。しかし、「いっちょんわからん。」「三平方の定理しか使いきらん。」という人は、次の方法を試してください。

【三平方の定理で解いてみる方法】

ポイントは、30゜、60゜の直角三角形はもとは正三角形であるというのを利用します。つまり、下の図のように考えてみます。このとき、$\color{red}{xは2y}$となります。あとは三平方の定理を利用します。

$ABは斜辺なので、三平方の定理を利用すると、\\y^2+3^2=x^2となります。\\ここで、xに2yを代入します。\\\begin{align}y^2+3^2&=(2y)^2\nonumber\\y^2&=4y^2-9\nonumber\\y^2-4y^2&=-9\nonumber\\-3y^2&=-9\nonumber\\y^2&=3\nonumber\\y&=\sqrt{3}\tag{y>0より}\end{align}$

$したがって、xは、次のように求められます。\\x=2yにy=\sqrt{3}を代入して、\\x=2 \times \sqrt{3}=2 \sqrt{3}$

以上。どうでしたか。$1:2:\sqrt{3}$が使えなくても、三平方の定理だけでもなんとかなりそうです。しかし、比が使えると楽なのは間違いないので、比の練習もしておきましょう。

次は、$1:1:\sqrt{2}$です。こちらへどうぞ。。。