一次関数と二次関数で囲まれた中にできる三角形の面積を「パッ」と出す方法です。
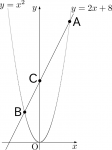
<問>図1のように曲線:$y=x^2$と直線:$y=2x+8$でが点A、点Bで交わっているとき、△OABの面積を求めよ。
- 図1
【前提条件】
- 三角形の面積を求めることができる。
- 交点の座標を求めることができる。
- (おまけ:等積変形を知っている。)
<手順>
- △OABを描く。
- 各交点(点A、点B、点C)の座標を書き込む。
- 点A、点Bを真下の$x$軸上へ移動し、△MCNをつくる。
- △MCNの面積を求める。
1.△OABを描く。
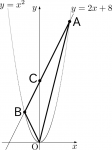
△OABを描きます。
- 図2:△OABを描く
2.各交点(点A、点B、点C)の座標を書き込む。
連立方程式を解きます。
\begin{eqnarray}
\left\{
\begin{array}{l}
\nonumber
y=x^{2}\\
y=2x+8
\end{array}
\right.
\end{eqnarray}
\begin{align} x^{2} & =2x+8 \nonumber \\x^{2}-2x-8 & =0 \nonumber \\(x+2)(x-4) & =0 \nonumber \\x=-2,x=4 \nonumber \end{align}
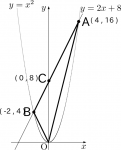
点A(-2,4)、点B(4,16)、点Cは、$y=2x+8$の切片なので、点C(0,8)となり、図の中に記入します。(図2)
- 図3:点A、点B、点Cの座標を記入
3.点A、点Bを真下の$x$軸上へ移動し、△MCNをつくる。
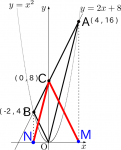
等積変形の考え方を利用します。点Aと点Bを真下の$x$軸上へ移動します。移動したそれぞれの点を点M(4,16)、点N(-2,4)とし、△MCNを描きます。この△MCNの面積と求めたい△OABの面積は等しいです。(等積変形により、△OMC=△OAC、△ONC=△OBC)
- 図4:点A、点Bをx軸上に移動し、点M、点Nとする。
4.△MCNの面積を求める。
△MCNの底辺はMN=2+4=6、高さはCO=8です。
\begin{align} \rm{△MCN} &=6 \times 8 \times \frac{1}{2} \nonumber \\ & = 24 \nonumber\end{align}
△MCNの面積は、24です。すなわち、△OABの面積は、24です。
=====================================================
普通は、△OABの面積を△OCAと△OCBに分けてそれぞれの面積を求め、それらを合わせます。