三平方の定理の続き（前回はこちら）です。

今度は、$1:1:\sqrt{2}$を使わずに、三平方の定理で解いてみます。

その前に、軽く三平方の定理の復習と$1:1:\sqrt{2}$の使い方を確認します。

１．三平方の定理の復習

三平方の定理とは、直角をはさむ２辺の長さと斜辺の長さとの関係です。つまり、

$a^2+b^2=c^2$

となります。ここで、ｃは斜辺です。

２．$1:1:\sqrt{2}$の使い方

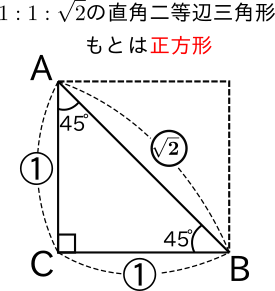
$1:1:\sqrt{2}$の辺の比を持つ直角三角形は、下図のような直角二等辺三角形です。

【例題１】下図の直角二等辺三角形の$x$の長さを求めなさい。

$AB:BC=\sqrt{2}:1より、$

\begin{align} \sqrt{2}:1&=4:x\nonumber\\\sqrt{2}x &= 4\nonumber\\ x &= \frac{4}{\sqrt{2}}=2\sqrt{2}\tag{答} \end{align}

３．三平方の定理だけで解いてみる

直角二等辺三角形なので、ACも$x$となります。これを利用して、解きます。

図５を参考にして、式をつくって解きます。

\begin{align}x^2+x^2 &= 4^2 \nonumber\\ 2x^2 &= 16 \nonumber\\ x^2 &= 8 \nonumber\\ x &= \sqrt{8} \tag{x > 0より} \\ x &= 2 \sqrt{2} \tag{答} \end{align}

どうでしょう。まぁ、三平方の定理でも解けますね。

しかし、もし、4ではなく0.4などの小数や分数が出た場合は、ちょっと計算が苦しくなります。

あくまでも、一時しのぎと考えて使ってください。本来は、比を利用するのがベストです。