円周率の3.14を使った計算ほど面倒くさいものはありませんね。今回は、3つの半円を組み合わせた問題で、計算を楽にやる方法を伝授します。
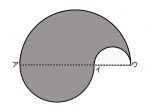
例題:図1で、アイの長さが6cm、イウの長さが4cmの半円を組み合わせた図形の色のついた部分□□□の面積を求めなさい。
- 図1:3つの半円を組み合わせた問題。
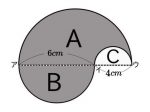
まずは、ふつうのやりかたで、解いてみます。半円のそれぞれ、A、B、Cに分けて考えます。
- 図2:半円A、B、Cに分けて考える。
そして、半円Aの面積+半円Bの面積−半円Cの面積が求める答えとなります。では、それぞれの面積を求めます。ここで、半円Aの直径が10cm(6+4なので)なので、半径は5cmです。
\begin{align} \rm{半円Aの面積} &= 5 \times 5 \times 3.14 \div 2 \nonumber \\ &=39.25(cm^2) \\ \rm{半円Bの面積} &= 3 \times 3 \times 3.14 \div 2 \nonumber \\ &= 14.13(cm^2) \\ \rm{半円Cの面積} &= 2 \times 2 \times 3.14 \div 2 \nonumber \\ &= 6.28(cm^2) \end{align}
\begin{align}\rm{(1)+(2)-(3)が求める面積になるので、}\nonumber\\ 39.25+14.13-6.28=47.1(cm^2) \nonumber \cdots\hspace{ 10px }(解) \end{align}
ここまでで、とっても面倒だなと思うのはふつうですね。なんとか、簡単に楽に計算したいですね。
【前提条件】
- 円の面積を求めることができる。
- 小数計算ができる。
<手順>
- 一つの式で表す。
- カッコ()を利用する。
1.一つの式で表す。
求める面積は、半円Aの面積+半円Bの面積−半円Cです。これを、一つの式で表すと、
$5 \times 5 \times 3.14 \div 2 + 3 \times 3 \times 3.14 \div 2 – 2 \times 2 \times 3.14 \div 2 =$
2.カッコ()を利用する。
1.の式をよーくながめてみると、$ \color{red}{ \times 3.14 \div 2 } $が同じです。この部分を利用します。
ここで、次の式を思い出してください。
$4 \times 5 + 3 \times 5 = (4+3) \times 5 = 7 \times 5 = 35$
$4 \color{red}{\times 5} + 3 \color{red}{\times 5} = (4+3) \color{red}{\times 5} = 7 \times 5 = 35$
同じ計算部分、ここでは、$ \color{red}{\times 5}$をあとで計算し、異なる部分、ここでは、$4+3$の部分をカッコ()で先に計算します。つまり、$(4+3) \times 5$となります。
では、本題に戻(もど)ります。$ \color{red}{ \times 3.14 \div 2 } $が同じ部分なので、あらためて面積を求める式をよくみてみます。
$5 \times 5 \color{red}{\times 3.14 \div 2} + 3 \times 3 \color{red}{\times 3.14 \div 2} – 2 \times 2 \color{red}{\times 3.14 \div 2} =$
ここで、$ \color{red}{ \times 3.14 \div 2 } $をあとに計算し、異なる部分、ここでは、$4 \times 4 + 3 \times 3 – 2 \times 2$の部分をカッコ()で先に計算します。つまり、次のように計算します。
\begin{align} & 5 \times 5 \color{red}{\times 3.14 \div 2} + 3 \times 3 \color{red}{\times 3.14 \div 2} – 2 \times 2 \color{red}{\times 3.14 \div 2} \nonumber \\ & = ( 5 \times 5 + 3 \times 3 – 2 \times 2 ) \color{red}{\times 3.14 \div 2} \nonumber \\ & = ( 25+9-4 ) \color{red}{\times 3.14 \div 2} \nonumber \\ & = 30 \times 3.14 \div 2 \\ & = 47.1(cm^2) \nonumber \end{align}
(4)の式では、$\times 3.14 \div 2$の計算が、1回だけです。どうです?楽でしょう。
コツは、一つの式で表してみることです。そうすると、式の中に計算のヒントが隠れています。今回のように、探してみましょう。