(3)図2は、図1において、辺ACを対象の軸として、点Eと対象な点Gをとり、点Gと点A、E、Cをそれぞれ結び、線分EGと辺ACとの交点をHとしたものである。
AD=3cmのとき、△DHGの面積を求めよ。
三角形の面積なので、$\displaystyle 底辺×高さ×\frac{1}{\;2\;}$ を利用して求めます。底辺、高さを求めます。もちろん、面積比から求めることも考えられますが、(2)の図形との関連性が全く無いようなので、直接、底辺や高さを求めます。また、正三角形なので、60゜、30゜の直角三角形の辺の比、$\displaystyle 1:2:\sqrt{3\;}$ も使えそうです。
では、さっそく求めます。
【前提条件】
- 辺の比、比例式を使うことができる。
- 仮定を図にすべて記入できる。
- 線対称な図形の特徴を理解している。
<手順>
- 仮定を図にすべて記入する。そのとき、線対称な図形の特徴を利用する。(辺の長さや角度に注目)
- 特別な三角形の辺の比を利用する。
- 三角形の面積を求める。
1.仮定を図にすべて記入する。そのとき、線対称な図形の特徴を利用する。
〔辺の長さに注目〕
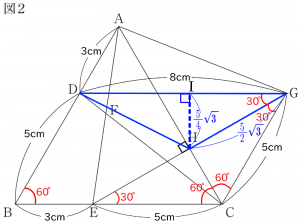
AD=3cmより、BD=5cm、BD=3cm、EC=5cmです。また、点Gは、点Eと線対称なので、GC=5cmとなります。
〔角度に注目〕
点Gは、点Eと線対称なので、△ACE≡△ACGより、∠ACE=∠ACG=60゜となります。
また、△CEGは辺CE=辺CGの二等辺三角形なので、∠CEG=∠CGE=30゜です。
また、∠ABC=60゜、∠ECG=120゜、BD=CG=5cmより、四角形DBCGは平行四辺形です。
したがって、∠DGE=∠GEC=30゜(平行線の錯角は等しい)です。
以上、すべてのことを画像7に記入します。
2.特別な三角形の辺の比を利用する。
△GCHは60゜、30゜の直角三角形なので、辺の比から
\begin{align}5 : \rm{GH} &= 2 : \sqrt{3\;}\nonumber\\2\rm{GH} &= 5\sqrt{3\;}\nonumber\\ \rm{GH} &= \frac{5}{\;2\;}\sqrt{3\;}\nonumber\end{align}
HIを△DHGの高さとします。△HGIは、60゜、30゜の直角三角形なので、辺の比から
\begin{align}\frac{5}{\;2\;}\sqrt{3\;} : \rm{HI} &= 2 : 1 \nonumber\\2\rm{HI} &= \frac{5}{\;2\;}\sqrt{3\;}\nonumber\\ \rm{HI} &= \frac{5}{\;4\;}\sqrt{3\;}\nonumber\end{align}
$\displaystyle △\rm{DHG}の高さ、\\\displaystyle\rm{(HI)}= \frac{5}{\;4\;}\sqrt{3\;}(cm)$
3.三角形の面積を求める。
$\displaystyle\rm{△DHG}の面積は、8 × \frac{5}{\;4\;}\sqrt{3\;} × \frac{1}{\;2\;} = 5\sqrt{3\;}(cm^{2})\cdots\hspace{ 10px }(解)$