平成28年度実施の、福岡県立高校入試の数学追加問題の大問2の解説です。
【問題2】1辺が8cmの正三角形ABCがある。
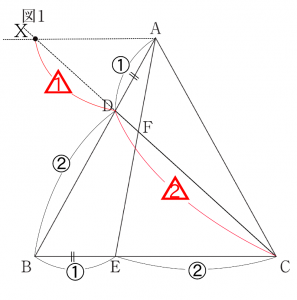
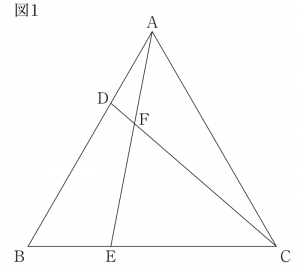
図1は、辺AB上に点A、Bと異なる点Dをとり、辺BC上にAD=BEとなるように点Eをとり、点Aと点E、点Cと点Dをそれぞれ結び、その交点をFとしたものである。
次の(1)は指示にしたがって、(2)、(3)は最も簡単な数で答えよ。
ただし、根号を使う場合は$\raise1ex\sqrt{\hspace{10pt}}$の中を最も小さい整数とすること。
 (1)は、省略。発表されている模範解答の通りです。
(1)は、省略。発表されている模範解答の通りです。
参考URL>>http://www.pref.fukuoka.lg.jp/contents/kensamondai28.html
(2) 図1において、AD:DB=1:2のとき、△FECの面積は、四角形DBEFの面積の何倍か求めよ。
<解説>「面積は何倍か…」とあるので、求める方法は大きく分けて2つあります。
1つ目は、直接面積を求める方法です。底辺や高さなどの長さを直接求めていきます。
2つ目は、「何倍」とあるので、「比」を利用する方法です。$面積比=(相似比)^{2}$ や「高さが等しい(頂点が共通)な三角形の底辺の比」(等積変形)を利用します。
大前提として、正三角形とあるので、有名な辺の比、$\rm{1:2:\sqrt{3\:}}$ と1辺の長さが8cmが指定されているので、長さを求めて面積を直接求めることができるかもしれませんが、直感的に2つ目の方法の比を利用します。なぜなら、もし、長さが求められるなら、比の方がはるかに簡単に求められるからです。実際には、2つ目の方法でも、長さを利用します。
2つ目の方法のポイントは、DF:FCを求めることです。この比がわかれば、等積変形で答えは簡単にでます。
<前提条件>
- 仮定を図1中に記入できる
- 相似比を理解している
- 等積変形が理解できる
- 比の操作ができる
<手順>
- 点Aを通り辺BCに平行な直線と、辺DCの延長線との交点をXとする。XD:DCを求める。
- XF:FCを求める。
- DF:FCを求める。
- △BFD:△BFCを求める。
- △FEB:△FECを求める。
- △FEC:四角形DBEFを求める。
1.点Aを通り辺BCに平行な直線と、辺DCの延長線との交点をXとする。XD:DCを求める。
DF:FCを求めるためには、相似な三角形が必要になります。すでに、(1)で、△ABE∽△AFDは証明されているので利用できますが、DF:FCには活用できそうにありません。そこで、新たに相似な三角形をつくることにしました。
それが、△ADXです。では、画像1を見ましょう。
AX//BCなので、△ADX∽△BDCです。相似比は、1:2です。(画像1の赤の△)
XD:DC=1:2
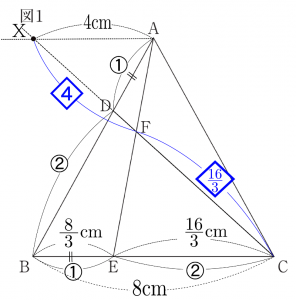
2.XF:FCを求める。
次は、XF:FCを求めます。△FAX∽△FECを利用します。(画像2を参考)
ここで、$\rm{BE:EC=1:2}、\rm{BC=8cm}より、\rm{BE=8 × \frac{\lower1ex\hbox{1}}{\raise1ex\hbox{3}}=\frac{\lower1ex\hbox{8}}{\raise1ex\hbox{3}},EC=8 × \frac{\lower1ex\hbox{2}}{\raise1ex\hbox{3}}=\frac{\lower1ex\hbox{16}}{\raise1ex\hbox{3}}}$
まず、△DAX∽△DBCよりAD:DB=AX:BC=1:2となり、BC=8cmなので、AX=4cmとなります。
△FAX∽△FECより、$\rm{AX:EC=4:\frac{\lower1ex\hbox{16}}{\raise1ex\hbox{3}}}$となります。
また、$\rm{XF:FC=4:\frac{\lower1ex\hbox{16}}{\raise1ex\hbox{3}}}$となります。(画像2を参考)
$\rm{XF:FC=4:\frac{\lower1ex\hbox{16}}{\raise1ex\hbox{3}}}$
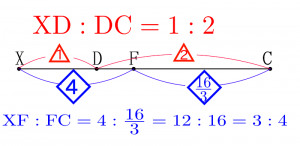
3.DF:FCを求める。
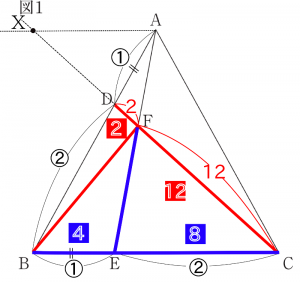
画像3より、XF:FC=3:4となります。
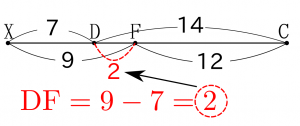
画像4より、DFの比を求めます。まず、XD:DC=1:2よりXCは3の長さ(または、3等分)と考えます。XF:FC=3:4よりXCは7の長さ(または、7等分)と考えられます。これらのことから、XCの長さを3と7の最小公倍数21とするとそれぞれの比を同じ意味を持つ比としてあつかえます。
ここで、$\rm{XD= 21 × \frac{\lower1ex\hbox{1}}{\raise1ex\hbox{3}}=7、XF= 21 × \frac{\lower1ex\hbox{3}}{\raise1ex\hbox{7}}=9となり、DF= 9 – 7 =2 となります。}$(画像4参考)
$\rm{DF:FC=2:12}$
4.△BFD:△BFCを求める。
「3」までで、下準備は完了です。では、さっそく面積比を求めていきましょう。
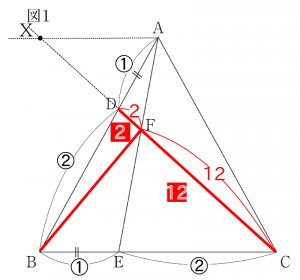
△BFD:△BFCを求めます。この2つの三角形の共通の頂点をBとすると底辺比が面積比になります。つまり、底辺DF:底辺CF=2:12なので、面積比も、△BFD:△BFC=2:12となります。(画像5を参考、赤い四角内の数字。)
(2:12=1:6ですが、面倒なのでそのまま利用します。お好みで簡単にして使っても構いません。その場合、5.以下の内容でも適宜変更して使ってください。例えば、△BFC=6などです。)
5.△FEB:△FECを求める。
同様に、△FEBと△FECについて、考えます。頂点Fが共通なので、底辺BEと底辺ECの比が面積比になります。BE:EC=1:2より、△FEB:△FEC=1:2です。ここで、「4」より、△BFC=12であることから、
$\rm{△FEB=12 × \frac{\lower1ex\hbox{1}}{\raise1ex\hbox{3}}=4、△FEC= 12 × \frac{\lower1ex\hbox{2}}{\raise1ex\hbox{3}}=8}$となります。(画像6を参考、青い四角内の数字)
4:8=1:2ですが、そうすると、せっかく比の意味を合わせているのが使えなくなるので、そのままにしておきます。
6.△FEC:四角形DBEFを求める。
いよいよ答えを求めます。
四角形DBEF=△BFD+△FEB=2+4=6です。△FEC=8です。したがって、△FEC:四角形DBEF=8:6です。
「△FECの面積は、四角形DBEFの面積の何倍か」を求めると、
$\displaystyle 8 ÷ 6 = \frac{\lower1ex 8}{\;\raise1ex 6\;}=\frac{\lower1ex 4}{\;\raise1ex 3\;}\cdots\hspace{ 10px }(解)$
(3)は、次ページです。