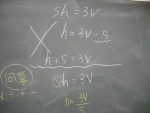志義ゼミナールは、福岡県小郡市の学習塾です。
小郡市はもちろん、近隣の鳥栖市、久留米市、筑紫野市からも通塾可能です。(西鉄沿線沿いなので。近隣駅は、西鉄小郡と大保駅です。)
おそらく、近隣の中学校でも中間考査が終わったころですね。みなさん、どうでしたか。
大原中は、24日・25日に中間考査が実施されました。まだ、結果は出ていませんが、思ったように得点できた人もいれば、残念な結果になった人もいます。
どちらにしても、大切なことは、『やり直し』をして、間違いの原因や対策を、しっかり施しておくことです。試験前の勉強も大切ですが、試験の後のやり直しも同じくらい重要です。
- もう少し冷静に考えよう!
- zuknowで暗記はバッチリ
- zuknowに問題を登録中
- 力の合成は、まず、作図です
- zuknowに登録中
例えば、中2数学の等式変形>>>>>>>>
Aくんは、次のように解きました……..
です。しかし、正解は、、、、、、、
です。
(1)では、「S」を移項しています。つまり、足し算と思っているようです。しかし、Aくんに確認するとSとhは掛け算だと言いい、それと同時に、間違いに気がつきました。しかし、そのあと、どのように計算するのかがわかりません。掛け算なので「S」を掛けると思っているようです。
私が、掛けているから、右側では(右辺では)割るんだよというと、もっと、不思議そうな顔をします。つまり、÷って?????
そうです、直ぐに(2)のような、数式\[h=\frac{3V}{S}\]を思いつかないのです。または、\[h=\frac{S}{3V}\]と考える人もいます。(分母と分子が逆になっているので、間違いです。まれにですが、文字式の場合、分母と分子の入れ替わりは同じ、と思っている中学生もいます。文字だからです。数字だと直ぐに違いに気づきます。)
正解できない原因が2つあるようです。
1つ目:掛け算であることを、忘れている。
2つ目:掛け算とわかっても、その後の計算がわからない。
以上のことから、等式変形が混乱していると思われます。一般的に、等式変形は、方程式と同じ仕組みで解くことができます。しかし、文字式の意味があいまいで、そのあつかいに不慣れな中学生に、単純に方程式と同じように解けますよとアドバイスしても意味がありません。
少し、乱暴ですが、「習うより、慣れろ」方式で、たくさん解いて練習します。できれば、短時間で解く練習をしてもらいます。そして、文字式のあつかいに慣れるのです。
では、最後に、これ、できます?(次のような、等式変形は、最難問です。)
解き方は、2つあります。お好きな方をどうぞ。
<解法1>
\begin{eqnarray} S & = & \frac{(a+b)h}{2} \nonumber \\ \frac{(a+b)h}{2} & = & S \tag{両辺を入れ替える} \\ (a+b)h & = & 2S \tag{両辺に2を掛ける。(分母の2が外れる)} \\ a + b & = & \frac{2S}{h} \tag{両辺をhで割る} \\ b & = & \frac{2S}{h} – a \tag{aを移項する。これが答え} \end{eqnarray}
<解法2>
\begin{eqnarray} S & = & \frac{(a+b)h}{2} \nonumber \\ \frac{(a+b)h}{2} & = & S \tag{両辺を入れ替える} \\ (a+b)h & = & 2S \tag{両辺に2を掛ける。(分母の2が外れる)} \\ ah + bh & = & 2S \tag{hを分配。a,bにそれぞれhをかけてカッコを外す} \\ bh & = & 2S – ah \tag{ahを移項する} \\ b & = & \frac{2S-ah}{h} \tag{両辺をhで割る。これが答え} \end{eqnarray}
解法1と解法2の答えが、全く違って見えるかもしれませんが、同じものです。(同じ意味を持つ式ということです。)
解法2の答えを少し変形してみると解法1の答えと同じになります。
\begin{eqnarray} b & = & \frac{2S-ah}{h} \nonumber \\ b & = & \frac{2S}{h}-\frac{ah}{h} \tag{hを分配。2Sとahをhで割る。} \\ b & = & \frac{2S}{h}-a \tag{ahのhが約分されて消える。これが答え} \end{eqnarray}
よく見ると、移項や両辺を同じ数で割ったり、かけたりするところは、方程式と同じルールを使っていることに気づくはずです。